syllogism

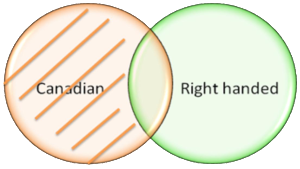
Venn diagrams are today’s mostly used method for solving syllogisms. With some practice they can be drawn fairly quickly making them a valuable tool in solving syllogisms in timed aptitude tests. Venn diagrams show all possible and hypothetically logical relations between a collection of finite and infinite statements. By means of an overlap between some certain assumptions conclusions can be made using the (in)finite statements. Two examples of the use of Venn diagrams will follow to clarify the above.

Example 1:

All Canadians are right handed
All right handed are opticians
Conclusion: Some opticians are Canadian

To check the validity of this statement first the different terms are appointed.

Subject:        Canadian
Predicate:      Optician
Middle term:    Right handed

We will start with the first out of the two given statements from above. The first thing to do is draw two circles and write the terms Canadian and Right handed in them. The circle with the word Canadian without the overlap represents only Canadian people, while the part within the overlap with the right handed circle represents all Right handed Canadian people. Everything outside these two circles represents everything not connected to these two terms. With this one can think of plants, animals, cars but even you and me.

Continue reading Venn diagram

Description

The basic form of the categorical syllogism is: If A is part of C then B is a part of C. (A and B are members of C).

Major premise

The major premise (the first statement) is a general statement of the form ‘All/none/some A are B’, for example:

All men are mortal.

This statement is not challenged and is assumed to be true.

Minor premise

The minor premise (the second statement) is also a statement about inclusion and is also assumed to be true. It is usually a specific statement, for example:

Socrates is a man.

It may also be a general statement with a reduced scope. Thus, for example, when the major premise takes the format of ‘all’, the minor premise may be ‘some’. The minor premise is also assumed to be true.

Conclusion

The conclusion is a third statement, based on a combination of the major and minor premise.

Socrates is mortal.

From the truth of the first two statements, a truth is created in this third statement. The trouble is that this ‘truth’ is not always true — yet it often appears to be quite a logical conclusion.