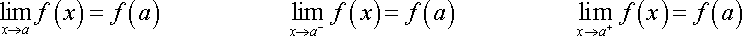Tag: limits

DEFINITION:

A function f is continuous at x = a if:

1)     f(a) exists, (The output at a exists.)

2)     The limit as x approaches a of f(x) exists, (The limit as "x approaches a" exists.)

3)     The limit is the same as the output.

A function is continuous over an interval if it is continuous at each point in that interval.

---

Continuity and 2 sided limits

If  is continuous at  x=a then,