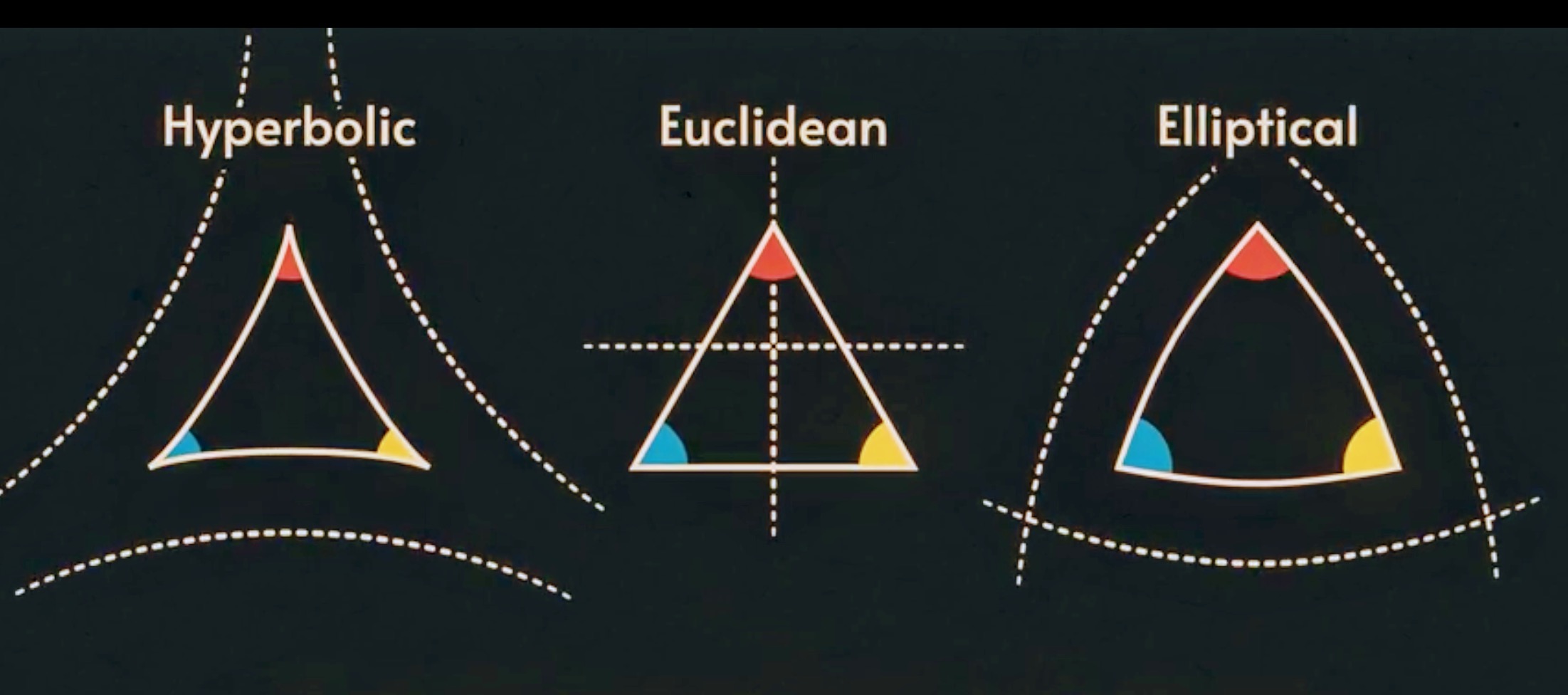
There are precisely three different classes of three-dimensional constant-curvature geometry: Euclidean, hyperbolic and elliptic geometry. The three geometries are all built on the same first four axioms, but each has a unique version of the fifth axiom, also known as the parallel postulate. The 1868 Essay on an Interpretation of Non-Euclidean Geometry by Eugenio Beltrami (1835 – 1900) proved the logical consistency of the two Non-Euclidean geometries, hyperbolic and elliptical.
The parallel postulate is as follows for the corresponding geometries.
Euclidean geometry: Playfair’s version: “Given a line l and a point P not on l, there exists a unique line m through P that is parallel to l.” Euclid’s version: “Suppose that a line l meets two other lines m and nso that the sum of the interior angles on one side of lis less than 180°. Then m and n intersect in a point on that side of l.” These two versions are equivalent; though Playfair’s may be easier to conceive, Euclid’s is often useful for proofs.
Hyperbolic geometry: Given an arbitrary infinite line l and any point P not on l, there exist two or more distinct lines which pass through P and are parallel to l.
Elliptic geometry: Given an arbitrary infinite line land any point P not on l, there does not exist a line which passes through P and is parallel to l.
Source and more info: https://en.m.wikibooks.org/wiki/Geometry/Hyperbolic_and_Elliptic_Geometry