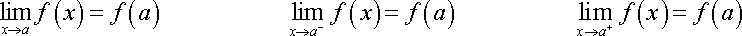DEFINITION:
A function f is continuous at x = a if:
1) f(a) exists, (The output at a exists.)
2) The limit as x approaches a of f(x) exists, (The limit as "x approaches a" exists.)
3) The limit is the same as the output.
A function is continuous over an interval if it is continuous at each point in that interval.
Continuity and 2 sided limits
If 
![]()
![]()